Le mot grec pour mesurer la terre est "géométrie".
Cette histoire commence il y a longtemps au pays d'Égypte (aidez les enfants à situer l'Égypte sur le globe).
Le seul endroit où la vie était possible se trouvait sur les rives d'un très grand fleuve. Sans ce fleuve, il aurait été impossible de vivre en Égypte.
Le fleuve était si important pour les habitants qu'ils l'appelaient tout simplement "le fleuve". Les eaux du grand fleuve Nil, coulent du sud au nord.
Le fleuve prend sa source dans des montagnes assez éloignées. Chaque année, au printemps, il pleut et il pleut dans ces montagnes lointaines. Toute l'eau des pluies ne peut pas être absorbée par la terre et une grande partie se jette dans le fleuve, qui s'élève très haut sur ses rives.
Lorsque les eaux atteignent l'Égypte, le fleuve déborde et inonde les champs avoisinants. On pourrait penser que ces inondations sont un désastre pour les Égyptiens. Non ! Ces inondations ont été une véritable bénédiction pour les habitants de l'Égypte dans les temps anciens.
Lorsque l'eau du fleuve franchissait les berges, elle charriait des débris et de la boue provenant des montagnes lointaines. Les eaux répandaient la riche boue noire, l'humus, sur les terres qu'elles inondaient. Il s'agissait d'un moyen naturel de fertiliser les terres agricoles.
La boue du Nil rendait les terres très fertiles. C'est pourquoi le fleuve était appelé "le don de l'Égypte". Mais les inondations causaient aussi des problèmes. Chaque année, les lignes de démarcation qui séparaient les champs d'un agriculteur de ceux de son voisin étaient détruites.
L'histoire de la géométrie par Maria Montessori.
Trois façons d'utiliser l'histoire dans votre classe :
1- Faire des recherches en posant des questions :
Les possibilités sont les suivantes :
- Pouvez-vous imaginer comment les Égyptiens ont pu utiliser une corde comme celle-ci pour mesurer la terre avec 4 personnes ?
- Avez-vous une idée de l'utilité des nœuds rouges ?
- Pouvez-vous trouver une solution ?
- Quelle forme avez-vous créée ?
- Êtes-vous capable de créer une autre forme ?
2. Nous avons besoin de 4 enfants et de 4 pions :
Les enfants tiennent la corde à l'endroit où les nœuds sont marqués.
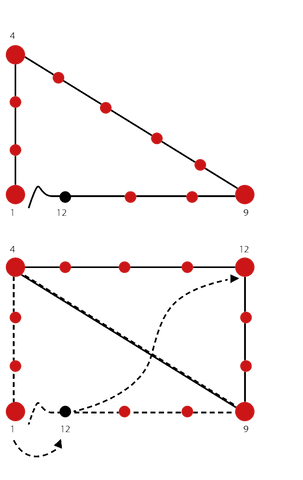
Sur une corde de 12 mètres, par exemple, il y a un nœud après chaque mètre, mais les nœuds 1, 4, 9 et 12 sont marqués d'une couleur ou d'une taille différente. La corde peut être nouée, mais il est préférable d'utiliser une corde non nouée.
Trois enfants forment d'abord un triangle (un triangle rectangle, pas un triangle équilatéral) : l'enfant 1 tient le début, l'enfant 2 tient le nœud 4, l'enfant 3 tient le nœud 9 et l'enfant 4 tient le nœud 12.
Après le nœud 12, il reste un morceau de corde qui doit être attaché au nœud 1. Ensuite, les nœuds 1, 4 et 9 seront marqués par des pions.
L'enfant 4 prend alors la corde au nœud 12 et reproduit toute la forme en marchant jusqu'au bord opposé.
Si la corde est nouée, l'enfant doit lâcher la corde, mais le marqueur reste. Si la corde n'est pas nouée, l'enfant 4 place le nœud 12 exactement au-dessus du nœud 9 et attache la dernière partie au nœud 4.
Ensuite, un pion doit être placé dans le coin supérieur droit, au nœud 12. Un rectangle parfait a été créé, marqué par des pions ou des enfants. Si vous faites cet exercice à l'extérieur, vous pouvez couvrir une plus grande surface.
3. Activité Matériel :
- Un morceau de corde (2 m ou plus)
- 12 perles
Le morceau de corde doit être divisé par des nœuds à 12 distances égales.
1- Commencez par un nœud ;
2- Ajoutez une perle ;
3- Faites un nœud juste après la perle pour qu'elle reste à sa place ;
4- Choisissez une perle pour le nœud.
Choisissez une distance de 10 cm ou plus ;
1- Faites un autre nœud ;
2- Une autre perle ;
3- Un autre nœud ;
4- Et mesurez à nouveau une distance similaire.